HOME»情報セキュリティスペシャリスト平成24年秋期»午前Ⅰ 問1
情報セキュリティスペシャリスト平成24年秋期 午前Ⅰ 問1
問1
全体集合S内に異なる部分集合AとBがあるとき,A∩Bに等しいものはどれか。ここで,A∪BはAとBの和集合,A∩BはAとBの積集合,AはSにおけるAの補集合,A-BはAからBを除いた差集合を表す。
- A-B
- (A∪B)-(A∩B)
- (S-A)∪(S-B)
- S-(A∩B)
分類 :
テクノロジ系 » 基礎理論 » 離散数学
正解 :
ア
解説 :
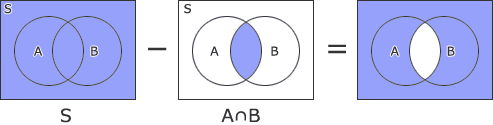
それぞれの演算をベン図で表すと次のようになります。
[問題文 A∩B]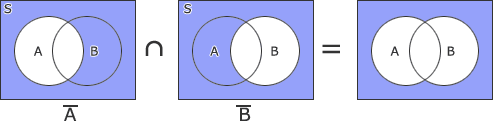
[問題文 A∩B]

- A-B
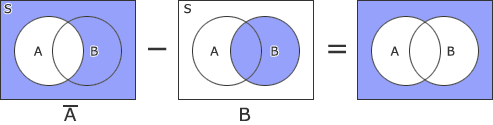
- (A∪B)-(A∩B)
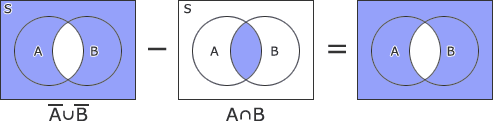
- (S-A)∪(S-B)
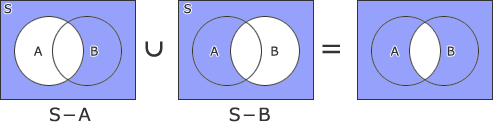
- S-(A∩B)
出典
- 応用情報技術者平成24年秋期 問1と同題
